As an undergraduate, I had more hair and less of a clue, and I fell under the spell of the mathematicians who view proof as a synthetic process guided by Cleverness. Proofs argued from the hypotheses forwards, and what made `forwards' coincide with `towards the desired conclusion' remained a sacred mystery guarded by an elite I was ultimately either too stupid or too lazy to join.
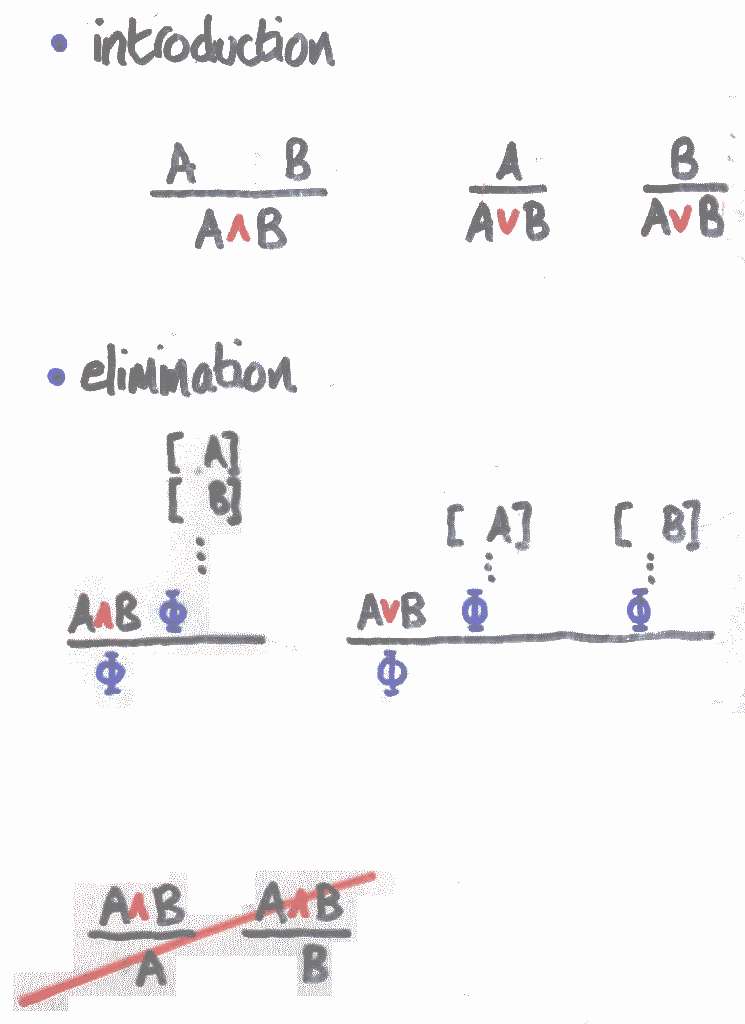
When I was taught natural deduction, I got the bizarre impression that the rules were intended to be applied in a forwards direction. (You too can give your undergraduates this impression if you make them learn discrete mathematics from Epp, Maurer and Ralston, or any of the other popular texts.) The two and-projections seemed sensible at the time, while or-elim seemed pretty odd. `Where does Phi come from?' I thought, `At least I can always project a conjunct each time I want one.'
It was only when I caught Tom Forster doing a proof on the blackboard from the bottom up that I got the message. Blimey! Phi is whatever it is you're trying to prove. Or-elim exploits a disjunction nomatter what the goal. Projecting from A/\B is no good at all, unless you're lucky enough to be trying to prove one of the two.
Throw and-projection in the bin, folks! Use the Phi version instead. Functional programmers call it `uncurrying'. Pascal programmers call it `with .. do'. I call it a rule you can use without knowing the answer beforehand, which in my case is most of the time.
Next: applying generic elim rules specifically | Prev: finite set elimination | Up: contents